Cp Cpk - zdolność procesu, wzory, interpretacja i zalecenia

Wprowadzenie

W przemyśle stosowanych jest wiele różnych wskaźników związanych z jakością procesów. Często spotykane to zdolność procesu (Cp, Cpk), wydajność procesu (Pp Ppk) oraz zdolność maszyn (Cm Cmk). Wymienione wskaźniki bazują na bardzo podobnych wzorach, a różnice występują w sposobie pobierania próbek lub we formule obliczającej odchylenie standardowe.

Wskaźniki zdolności i wydajności są powiązane z metodą SPC. Warto także wspomnieć, że Analiza MSA wykorzystuje wskaźniki Cg i Cgk w ramach tzw. badania Typu I.

Niniejszy artykuł przedstawia ideę zdolności procesu, typowe wzory, interpretację wyników oraz zalecenia ułatwiające ich analizę.

Zdolność procesu - idea

Zdolność procesu pomaga ocenić stopień, w jakim wyniki danej charakterystyki zebrane z procesu mieszczą się w określonych granicach specyfikacji. Jest to swego rodzaju porównanie "granic" procesu z limitami specyfikacji. Na tej podstawie można ocenić, czy proces spełnia wymagania specyfikacji.

W przemyśle przyjęto zasadę, w której te "granice" procesu to zakres wartości zawierający 99,73% wyników. Dla rozkładu normalnego będzie to rozumiane jako ±3 odchylenia standardowe (σ) od średniej (X).

Podsumowując - intencją wskaźników Cp i Cpk jest określenie, czy proces jest zdolny do spełniania wymagania klienta.[1]

Cp, Cpk - wzory

Podane poniżej wzory są najczęściej spotykane w przemyśle i opierają się o zasady podane w podręczniku AIAG SPC[1]. Formuły te są użyteczne dla procesów statystycznie stabilnych i jednocześnie posiadających rozkład normalny lub zbliżony do normalnego.

Dla procesów o rozkładzie znacząco innym niż rozkład normalny, obliczenie wskaźników Cp i Cpk w oparciu o poniższe wzory nie będzie prawidłowe. W takich przypadkach należy zastosować inne podejście, wykraczające poza zakres tego artykułu.

Cp

Cp to wskaźnik przedstawiający potencjalną zdolność procesu, którą teoretycznie można by osiągnąć przy idealnym wycentrowaniu procesu względem granic specyfikacji. Wzór dla Cp:[1]

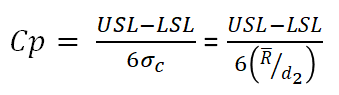
gdzie:

• USL - Górny limit specyfikacji (Upper Specyfication Limit)
• LSL - Dolny limit specyfikacji (Lower Specyfication Limit)
• σ_C - Estymator odchylenia standardowego, który jest obliczony ze średniego rozstępu (R) podzielonego przez stałą d2 zależnego od liczby elementów w podgrupie.

Cpk

Cpk to wskaźnik przedstawiający zdolność procesu z uwzględnieniem przesunięcia w kierunku jednej z granic specyfikacji. Dla tego wskaźnika wykonujemy dwa oddzielne obliczenia i następnie wybieramy mniejszy wynik. Wzór dla Cpk:[1]

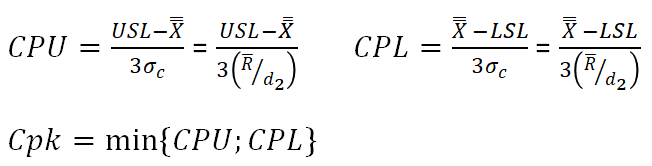
gdzie:

• USL - Górny limit specyfikacji (Upper Specyfication Limit)
• LSL - Dolny limit specyfikacji (Lower Specyfication Limit)
• Xśr - Średnia procesu
• σ_C - Estymator odchylenia standardowego, który jest obliczony ze średniego rozstępu (R) podzielonego przez stałą d2 zależnego od liczby elementów w podgrupie.

Odchylenie standardowe

Do obliczenia wskaźników Cp i Cpk stosuje się estymator odchylenia standardowego. Jest to przybliżenie rzeczywistej wartości odchylenia standardowego populacji, obliczane na podstawie próbek pobranych z tej populacji.

gdzie:

• R - średni rozstęp
• d2 - stała zależna od liczby elementów w podgrupie (n)

Cp, Cpk - interpretacja

Interpretacja wyników zależy od przyjętych zasad. Stosuje się specyficzne wymagania danego klienta lub jeżeli takowych brak, to typowo stosuje się jeden z wybranych standardów przemysłowych. Najczęściej stosuje się próg 1.67, czasami 1.33 lub 2.0.

Przykładowe zasady:

• Cp,Cpk ≥ 1.67: Proces spełnia wymagania klienta.
• 1.00 ≤ Cp,Cpk < 1.67: Proces wymaga doskonalenia; akceptacja zależna od klienta.
• Cp,Cpk < 1.00: Proces nie spełnia wymagań.

Wskaźniki Cp oraz Cpk należy analizować razem, gdyż ich wzajemna relacja wskazuje na możliwy kierunek doskonalenia procesu.

Poniższa animacja przedstawia relację między Cp i Cpk, kiedy proces zmienia swoje położenie lub swoją szerokość (zmienność):

Cp, Cpk - zalecenia

Poniżej kilka subiektywnie dobranych :) zaleceń, o jakich warto pamiętać:

• Ważna jest ilość próbek. Im więcej próbek zostanie zebranych, tym wynik Cp i Cpk będzie bardziej miarodajny, ponieważ obliczenie odchylenia standardowego oraz średniej procesu będzie zbliżał się do prawdziwych wartości całej populacji. W tym zakresie warto zgłębić pojęcie "przedział ufności" (ang. Confidence Interval).
• Proces ma rozkład zbliżony do normalnego. Formuły stosowane w obliczeniu wskaźnika Cp i Cpk zakładają rozkład normalny procesu. Jeżeli dana mierzona charakterystyka znacząco odbiega od takiego modelu, to obliczenia Cp i Cpk będą błędne. Istnieją metody obliczenia Cp i Cpk dla takich procesów, ale to wykracza to poza zakres tego artykułu.
• Proces powinien być statystycznie stabilny. Analiza zdolności procesu, który nie jest stabilny jest bez sensu. Wyniki obliczeń będą niepoprawne i nie mają znaczenia.
• Nie pomylić obliczeń z Pp, Ppk. To dość częsty błąd osób stosujących Excel z niesprawdzonymi formułami. Omyłkowo stosowany jest wzór na odchylenie standardowe z całej populacji, co powoduje obliczenie Pp i Ppk zamiast Cp i Cpk.
• Zdolny system pomiarowy. Jeżeli system pomiarowy jest niezdolny (ma dużą zmienność), to ta zmienność może znacząco pogorszyć rezultaty Cp i Cpk. Więc system pomiarowy powinien być zdolny. Więcej informacji znajdziesz w artykule: MSA - co to jest Analiza Systemów Pomiarowych?

Standardy

Wskaźniki Cp i Cpk są opisane w różnych standardach branżowych i normach międzynarodowych. Poniżej główne z nich:

• AIAG SPC. "Statistical Process Control (SPC)" Reference Manual
• ISO 22514 (series). "Statistical Methods in Process Management - Capability and Performance"
• AESQ AS13006. "Process Control Methods"

Podsumowanie

Wskaźniki zdolności procesu Cp i Cpk pozwalają na sprawdzenie, czy dany proces ma potencjał w spełnianiu wymagań klienta. Kryteria ich oceny powinny opierać się o ustalone z klientem wymagania.

Warto zawsze pamiętać, że wskaźniki Cp i Cpk mają sens, jeżeli dane użyte w obliczeniach są poprawne, czyli: pobrano odpowiednią ilość próbek, rozkład procesu jest normalny, proces jest stabilny, przyrząd pomiarowy wprowadza małą zmienność.

W tym kontekście mogą pojawić się problemy. Zdarza się, że inżynierowie próbują obliczyć wskaźniki Cp i Cpk na podstawie partii próbnej obejmującej zaledwie kilka sztuk, lub proces nie jest jeszcze statystycznie stabilny, a analiza MSA zostaje przeprowadzona "później".

Dlatego ważne jest, aby przed obliczeniem wskaźników upewnić się, że wszystkie warunki zostały spełnione. Poprawne podejście do analizy zdolności procesu nie tylko minimalizuje ryzyko błędnych wniosków, ale także przyczynia się do budowy zaufania i efektywnej współpracy z klientem.