Pp Ppk - wydajność procesu, wzory, interpretacja i zalecenia

Wprowadzenie

W przemyśle wykorzystuje się wiele wskaźników, które służą do oceny stopnia spełniania wymagań klienta. Analizie poddawane są m.in. aspekty finansowe, terminowość, wydajność oraz jakość. W ramach zarządzania jakością funkcjonuje szeroki wachlarz takich wskaźników, jak na przykład PPM, FTPY czy DPMO.

Jednak istnieje także specyficzna grupa wskaźników skoncentrowana na weryfikacji, czy wybrana charakterystyka produktu lub procesu spełnia wymagania klienta. W tym kontekście najczęściej stosowane wskaźniki w inżynierii jakości to:

• Pp, Ppk - wydajność procesu
• Cp Cpk - zdolność procesu
• Cm Cmk - zdolność maszyn
• Cg, Cgk - zdolność przyrządu pomiarowego

Warto pamiętać, że wskaźniki Pp, Ppk, Cp, Cpk, a także Cm i Cmk stanowią część znacznie szerszego tematu, jakim jest SPC (Statistical Process Control). Natomiast wskaźniki zdolności przyrządu pomiarowego Cg i Cgk są związane z analizą MSA (Measurement System Analysis).

Tematem niniejszego artykułu są wskaźniki wydajności procesu Pp oraz Ppk.

Wydajność procesu - idea

Wydajność procesu pozwala ocenić, w jakim stopniu dana charakterystyka produktu lub procesu mieści się w określonych granicach specyfikacji. Można więc uznać, że jest to forma oceny stopnia spełniania wymagań klienta.

Idea wskaźników Pp i Ppk polega na porównaniu wymagań klienta (specyfikacji) z tzw. "granicami procesu".

Poniższy rysunek przedstawia proces, którego rozkład mieści się w granicach specyfikacji oznaczonych pionowymi czerwonymi liniami. Dolna granica specyfikacji to LSL (ang. Lower Specification Limit), a górna to USL (ang. Upper Specification Limit). Natomiast "granice procesu" wyznaczono pomiędzy 0,135 i 99,865 percentylem co oznacza, że 99,73% obserwacji znajduje się w tym przedziale (99,865 - 0,135 = 99,73).

Jeżeli proces ma rozkład normalny, to 0,135 percentyl odpowiada wartości Xśr - 3σ, i jednocześnie 99,865 percentyl odpowiada wartości Xśr + 3σ. Dlatego przyjmuje się, że typowe granice procesu są rozumiane jako ±3σ od średniej procesu Xśr. Łącznie mamy więc proces o całkowitej szerokości 6σ.

Jeżeli proces nie ma rozkładu normalnego, to obliczenie wskaźnika Ppk w oparciu o Xśr±3σ będzie błędne. W takim przypadku należy zastosować alternatywne podejście, takie jak transformacja Co-Box, transformacja Johnsona, analiza percentyli itp.

Najczęściej wykorzystywaną metodą jest dopasowanie matematycznego modelu rozkładu do faktycznych danych. Następnie wyznacza się wartości dla 0,135 oraz 99,865 percentyla za pomocą funkcji odwrotnej dystrybuanty (F^-1), charakterystycznej dla danego rodzaju rozkładu. Te wyznaczone wartości określają "granice procesu" i są następnie zastosowane do obliczenia wskaźników Pp i Ppk.

Obecnie obliczenia tego typu są zazwyczaj realizowane za pomocą specjalistycznych programów statystycznych. Niemniej jednak, można je także przeprowadzić w arkuszach kalkulacyjnych lub przy wykorzystaniu bibliotek dostępnych w popularnych językach programowania, takich jak Python, R czy JavaScript.

Pp, Ppk - wzory

Przedstawione poniżej wzory są podane w podręczniku AIAG SPC[1]. Formuły te są użyteczne dla procesów posiadających rozkład normalny lub zbliżony do normalnego.

Pp

Pp to wskaźnik przedstawiający potencjalną wydajność procesu, którą teoretycznie można by osiągnąć przy idealnym wycentrowaniu procesu względem granic specyfikacji. Wzór dla Pp:[1]

gdzie:

• USL - Górny limit specyfikacji (Upper Specyfication Limit)
• LSL - Dolny limit specyfikacji (Lower Specyfication Limit)
• σ_P , s - Odchylenie standardowe

Ppk

Ppk to wskaźnik przedstawiający wydajność procesu z uwzględnieniem przesunięcia w kierunku jednej z granic specyfikacji. Dla tego wskaźnika wykonujemy dwa oddzielne obliczenia i następnie wybieramy mniejszy wynik. Wzór dla Ppk:[1]

gdzie:

• USL - Górny limit specyfikacji (Upper Specyfication Limit)
• LSL - Dolny limit specyfikacji (Lower Specyfication Limit)
• X̄ - Średnia procesu
• σ_P , s - Odchylenie standardowe

Odchylenie standardowe

Do obliczenia wskaźników Pp i Ppk stosuje się odchylenie standardowe. Jest to przybliżenie rzeczywistej wartości, obliczane z wszystkich pobranych próbkek (ang. Total Variation). Wzór:[1]

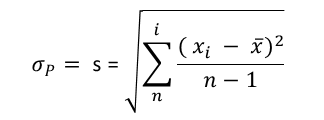
gdzie:

• x_i - Pojedyncza obserwacja w zestawie danych
• x̄ - Średnia arytmetyczna wszystkich obserwacji
• n - Całkowita liczba obserwacji w zestawie danych
• i - Indeks (numer obserwacji)

Pp, Ppk - interpretacja

Interpretacja wyników zależy od przyjętych zasad. Najczęściej stosuje się wymagania danego klienta lub jeżeli takowych nie ma, to ustala się własne limity. Bardzo często są to zasady podobne lub identyczne do tych, które stosuje się dla wskaźników zdolności procesu Cp Cpk. Najczęściej stosuje się próg 1.67, czasami 1.33 lub 2.0.

Przykładowe zasady:

• Pp,Ppk ≥ 1.67: Proces spełnia wymagania klienta.
• 1.00 ≤ Pp,Ppk < 1.67: Proces wymaga doskonalenia; akceptacja zależna od klienta.
• Pp,Ppk < 1.00: Proces nie spełnia wymagań.

Wskaźniki Pp oraz Ppk należy analizować razem, gdyż ich wzajemna relacja wskazuje na możliwy kierunek doskonalenia procesu.

Poniższa animacja przedstawia relację między Pp i Ppk, kiedy proces zmienia swoje położenie lub swoją szerokość (zmienność):

Różnica między Pp, Ppk a Cp, Cpk

Wskaźniki Pp i Ppk oraz Cp i Cpk różnią się sposobem obliczania odchylenia standardowego.

• Pp, Ppk wykorzystują odchylenie standardowe obliczane na podstawie zmienności całego procesu (tzw. "Overall variation"), z użyciem klasycznego wzoru uwzględniającego korektę przez n-1. Ten sposób liczenia odchylenia standardowego uwzględnia wszystkie źródła zmienności w procesie. Wskaźniki te są zatem bardziej reprezentatywne dla rzeczywistej, całkowitej zmienności procesu.
• Cp, Cpk bazują na odchyleniu standardowym wyliczonym przy użyciu estymatora R/d2, czyli bazuje na średniej z rozstępów podgrup (tzw "Within variation" ). Takie podejście pomija wpływ zmienności długoterminowej. Wskaźniki Cp i Cpk mierzą więc teoretyczną zdolność procesu, kiedy zmienność między grupami zostałaby wyeliminowana. Cp/Cpk skupia się na tym, czy proces jest wystarczająco powtarzalny i poprawnie zlokalizowany względem limitów specyfikacji, czyli co jest zdolny osiągnąć.

W praktyce możemy tak tą kwestię podsumować:

• Pp, Ppk wskazują, jak faktycznie działa proces. Uwzględnia całkowitą zmienność.
• Cp, Cpk wskazują, jak zdolny może być proces. Uwzględnia tylko część zmienności - wewnątrz podgrup.
• Pp ≤ Cp, Ppk ≤ Cpk. Wskaźniki Pp, Ppk nie mogą być większe niż Cp, Cpk jeżeli są obliczone z tych samych danych.
• Duże rożnice między Cp, Cpk a Pp, Ppk wskazują na występowanie zaburzeń w procesie, tj wystepują przyczyny specjalne.
• Zbliżone wartości między Cp, Cpk a Pp, Ppk sugerują, że proces jest statystyczenie stabilny, przyczyny specjalne nie występują lub mają znikomy wpływ.

Pp, Ppk - zalecenia

Poniżej kilka wskazówek, oczywiście subiektywnie ;) dobranych:

• Ważna jest ilość próbek. Im więcej próbek, tym bardziej miarodajny będzie wynik Pp i Ppk, ponieważ obliczenia będą bardziej zbliżały się do prawdziwych wartości całej populacji. W tym zakresie warto zgłębić pojęcie "przedział ufności" (ang. Confidence Interval).
• Obliczenie zależy od rodzaju rozkładu. Obliczenie Pp i Ppk może bazować na średniej procesu i odchyleniu standardowym, kiedy proces ma rozkład normalny lub przynajmniej zbliżony do normalnego. W przeciwnym przypadku należy zastosować inne zasady - np. dopasowanie modelu rozkładu do danych i następnie wyznaczenie percentyli.
• Nie należy mylić obliczeń z Cp i Cpk. To dość częsty błąd popełniany przez osoby stosujące Excel z niesprawdzonymi formułami.
• Zdolny system pomiarowy. Jeżeli system pomiarowy jest niezdolny (ma dużą zmienność), to ta zmienność może znacząco pogorszyć rezultaty Pp i Ppk. Więc system pomiarowy powinien być zdolny. Więcej informacji znajdziesz w artykule: MSA - co to jest Analiza Systemów Pomiarowych?

Standardy

Wskaźniki Pp i Ppk są opisane w różnych standardach branżowych i normach międzynarodowych. Poniżej główne z nich:

• AIAG SPC. "Statistical Process Control (SPC)" Reference Manual
• ISO 22514 (series). "Statistical Methods in Process Management - Capability and Performance"
• AESQ AS13006. "Process Control Methods"

Podsumowanie

Wydajność procesu Pp i Ppk to przydatne wskaźniki do oceny, czy dana charakterystyka spełnia wymagania klienta. Znajomość tych wskaźników oraz zrozumienie zasad ich poprawnego obliczania to bardzo ważny aspekt pracy inżyniera.

Czasami spotykam się z błędem polegającym na tym, że wskaźniki Pp i Ppk obliczono na podstawie modelu rozkładu normalnego, podczas gdy faktyczny proces ma rozkład zupełnie inny. Analiza takich wyników prowadzi później do błędnych wniosków i nieporozumień.

Posługując się wskaźnikami Pp i Ppk, warto także zwrócić uwagę na liczbę pomiarów (im więcej, tym lepiej), zdolność systemu pomiarowego (MSA) oraz poprawność stosowanych formuł.

Wydajność procesu powinna być regularnie monitorowana, a w przypadku spadku wskaźników należy podejmować działania doskonalące.